Completed Projects
Control Scheme in Swarm Operations Based on Game Theory
In a swarm competition scenario, the real-time decision-making problem in terms of task assignment and motion control is hard to address. For example, two groups of intelligent agents, which have different goals in a non-cooperative environment, are seeking proper control schemes to make reliable decisions.
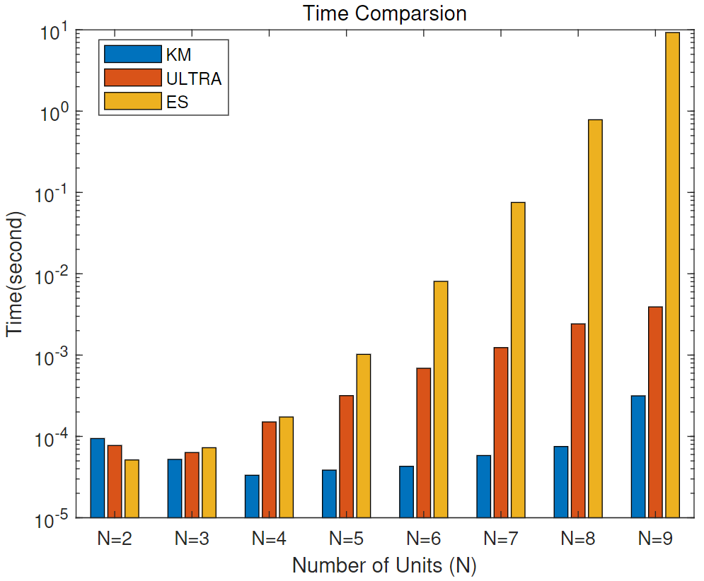
I applied the matrix-game-based model and developed a fast and optimal search algorithm to solve the decision-making problem. More specifically, I applied the Action-Reaction Search (ARS) method to find the Nash equilibriums in a large-scale payoff matrix without calculating the matrix’s all elements. Besides, the target assignment problem involved was solved by using a classic maximum weighted matching algorithm - the Kuhn-Munkres algorithm.
 |  |
It’s difficult to find optimal solutions all the time - sometimes, we just need to obtain a not-so-bad outcome. And that is what game theory can bring to us: it guarantees an optimal result under worst cases. By applying the matrix game, however, another issue arose - the combination of agents’ strategies became so large that the Nash equilibriums couldn’t be computed quickly. ARS solved such a problem through alternating row and column search, and Nash equilibriums can be calculated quickly.
The simulation process went satisfyingly well, and the project result dramatically improved – the computing speed for a single process step decreased from more than 50 seconds to 0.5 seconds.
Something interesting: I was walking alone the night before we found the ARS, thinking about the solution to the problem. With a flash of inspiration, I came up with a search method and then verified its effectiveness. However, when I read a thesis a few days later, I surprisingly found that the ARS method in this article was identical to my idea.
A Parallel Algorithm of the Control Scheme in Swarm Operations
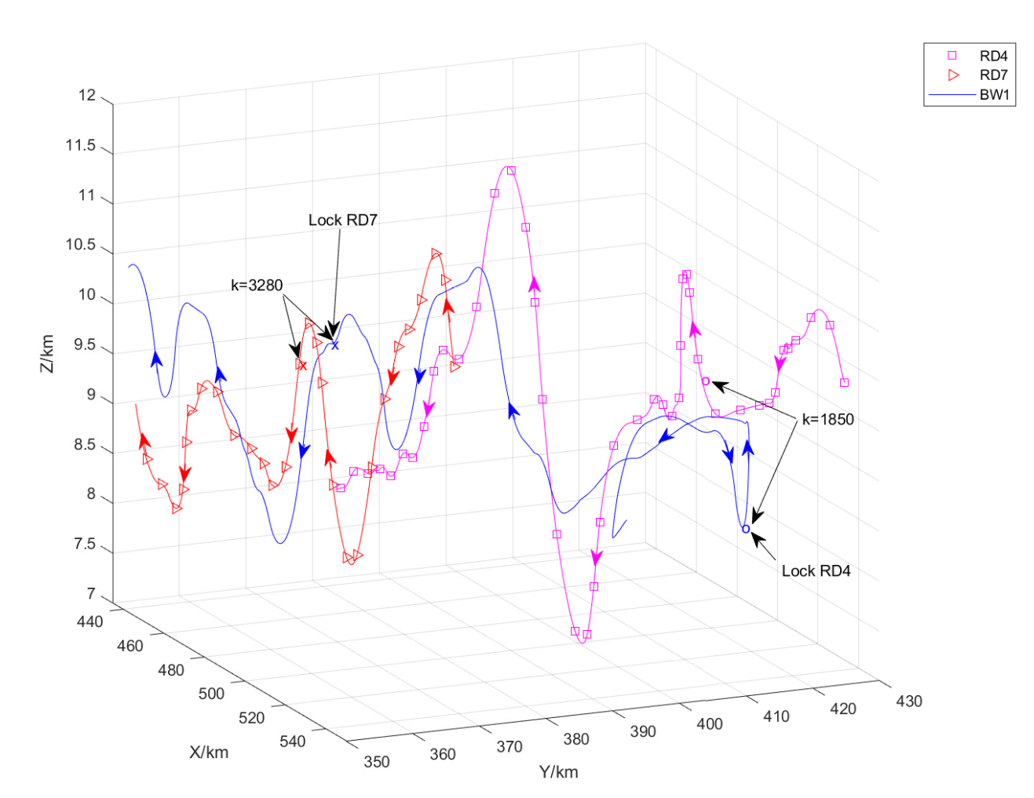
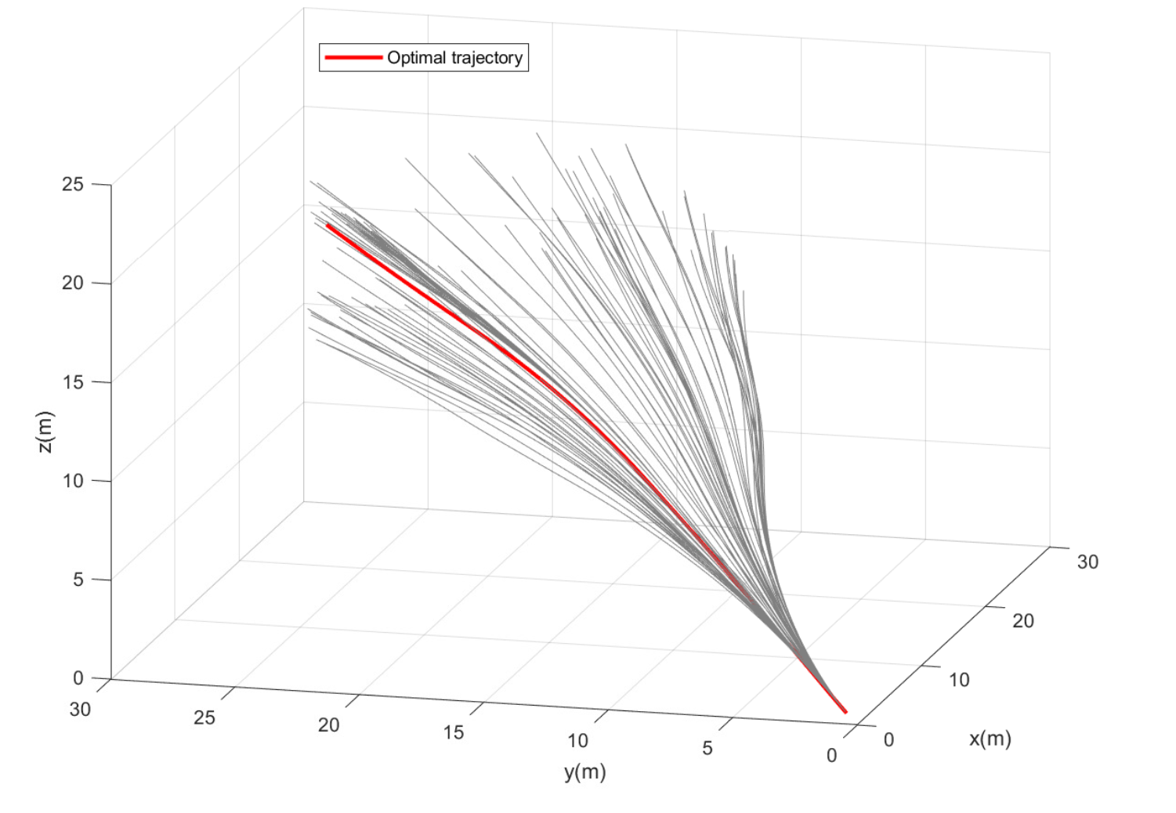
Based on the previous work, I further developed a parallelized/distributed control scheme for competing clusters with more complex dynamic systems, mainly in terms of parallelization of the Nash strategies search and target assignment algorithm, to achieve a faster and near-optimal decision-making process.
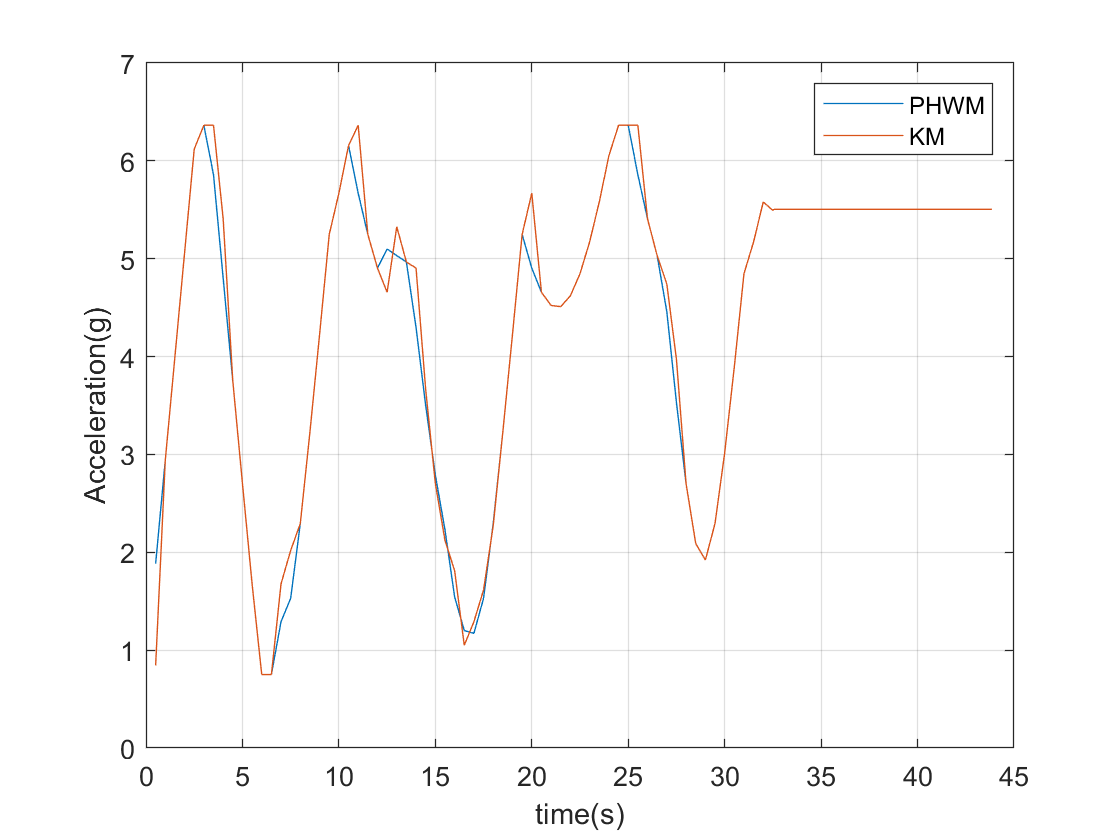
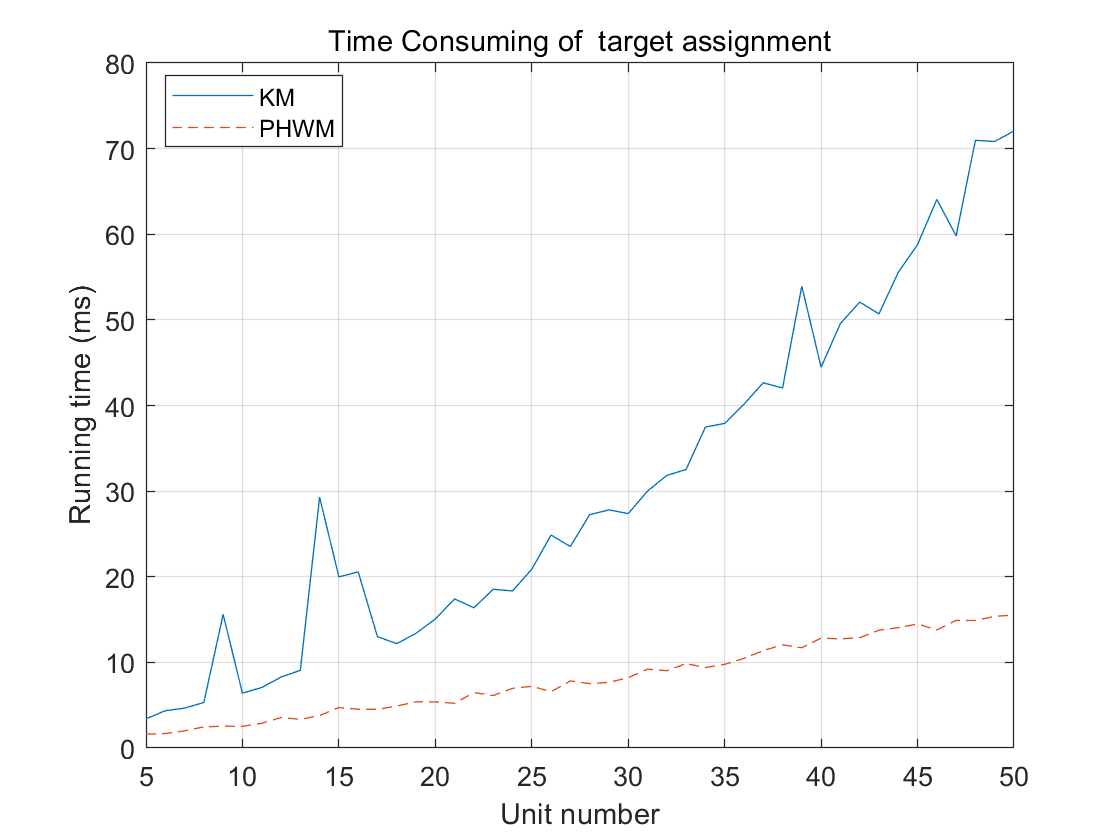
The ARS algorithm was easy to parallelize, while the parallelization of the target assignment scheme was pretty tricky. Like many parallel resource allocation algorithms, distributed target assignment was hard to parallelize while maintaining optimality but could achieve near optimal. Therefore, a feasible way was to reach the balance between computing speed and optimality, which led to my proposed algorithm - Parallel Heavy Weight Matching (PHWM). By calculating a perfect match and then optimizing the weight of the matching locally with augmenting circles, a near-optimal target assignment could be achieved.
The proposed scheme is proved to be optimal with a guaranteed 1/3-Nash solution and rapid computational speed - dozens of times faster than the KM algorithm with high accuracy - a 0.05 second of computing speed for a single process step even if the agent number reaches 100.
 |  |  |
